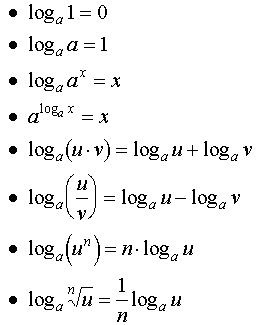4. FUNCIONES DE VARIABLE REAL

4.1 DEFINICIÓN, DOMINIO Y RANGO

Sean X y Y dos conjuntos no vacíos, subconjuntos de los números reales. Una función de variable real de X en Y es una regla de correspondencia que asocia a cada elemento de X un único elemento de Y. Esto se representa simbólicamente por: 

     f: X→Y

        x→y=f(x)

A la variable x se le llama variable independiente y a la variable y se la conoce como variable dependiente.

DOMINIO

Sea f una función de variable real f: X → Y. El conjunto X para el cual se encuentra definida, constituye el dominio de la función. Este conjunto se representa simbólicamente por dom f.

RANGO

Sea f una función de variable real f: X → Y, el conjunto de todas las imágenes de los elementos del dominio, constituye el rango de la función. Este conjunto se representa simbólicamente por rg f.

EJEMPLO 1  : 

*puedes definir una función f(x)=2x con dominio y codominio los enteros (porque tú lo eliges así).

Pero si lo piensas, verás que el rango (los valores que salen de verdad) son sólo los enteros pares.

Así que el codominio son los enteros (lo has elegido tú) pero el rango son los enteros pares.

EJEMPLO 2: 
*En una escuela hay 10 salones numerados del 1 al 10. Mediante una función le asignamos un salón a cada niño. A Juan le corresponde el Salón 1 y a Pedro el Salón 7. Esa es la función.

4.2 REPRESENTACIÓN GRÁFICA DE FUNCIONES 

La gráfica de una función está formada por el conjunto de puntos (x, y) cuando x varía en el dominio D.
gráfica (f) = {(x, f(x)) /  x ∈ D}
Para representarla calcularemos aquellos puntos o intervalos donde la función tiene un comportamiento especial, que determinaremos mediante el estudio de los siguientes apartados.

EJEMPLO 3 :

Como sabemos, el denominador no puede ser igual a cero, porque la función no tendría solución, luego lo  primero que haremos es Igualar a cero el denominador para establecer que valores arrojan como valor cero:  

2x2 – 8 = 0  

2x2 = 8  

x2 = 8/2 

x2 = 4

de donde obtenemos que las raices son : X = -2 y X = 2. Estos son los valores para los cuales no está definido el denominador. 

Entonces, El dominio estará formado por todos los reales excepto los números “2” y “ -2”
Dom f(x) = R – {-2,2} ; (– ∞ , -2) U (-2,2) U (2 , + ∞ )

Tabulamos algunos valores para graficar nuestra función. 

                         



                                

4.3 TIPOS DE FUNCIONES

4.4 FUNCIONES LINEALES 

Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.

La función lineal se define por la ecuación f(x) = mx + b ó y = mx + b llamada ecuación canónica, en donde m es la pendiente de la recta y b es el intercepto con el eje Y.

Por ejemplo, son funciones lineales f(x) = 3x + 2 g(x) = - x + 7 h(x) = 4 (en esta m = 0 por lo que 0x no se pone en la ecuación).

EJERCICIO 4:

 Determinar Dominio y Rango de  f(x) = X + 3 

Lo primero que hacemos es tabular valores de los pares ordenados x,y para representarlos
en el plano cartesiano:

Ahora ubicamos cada pareja en el plano y unimos los puntos para obtener la gráfica de nuestra función.

                         

Como podemos ver, la gráfica es una línea recta. Este tipo de función se conoce como lineal y representa a los polinomios de grado 1. 

Dominio de la función

Como es una función lineal el dominio será todo el conjunto de los números reales (puede tomar cualquier valor negativo o positivo sin restricción alguna). 

Dom f(x) = R      o también puede expresarse Dom  f(x) = (– ∞ , + ∞ )

Rango de la función

El Rango será también todo el conjunto de los números reales. Seguimos el eje “Y” de abajo hacia arriba y podemos leer valores siempre. 

Rango = (– ∞ , + ∞ ) 

EJEMPLO 5:

  *y = - 3x + 4
Vamos a hacerlo con dos valores de x para que sepas de donde salen los valores.

       Para x = - 1, y = -3(-1)+ 4 =  7  quedando la pareja (-1 , 7)

       Para x =  2,  y = -3(2) + 4 = -2   quedando la pareja (2 , -2)

X	y = - 3x + 4
-1	7
0	4
1	1
2	-2
3	-5

EJEMPLO 6 :

       *y = 2x

Vamos a hacerlo con dos valores de x para que sepas de donde salen los valores.

       Para x = - 2, y = 2(-2) = -4  quedando la pareja (-2 , -4)

       Para x =  1,  y = 2(1)  =  2   quedando la pareja (1 , 2)

X	y = 2x
-2	-4
-1	-2
0	0
1	2
2	4

EJEMPLO 7 :

*x = −5

EJEMPLO 8: 

*y = -3x -1

x	y = −3x − 1
0	-1
1	−4

4.5 FUNCIONES CUADRÁTICAS

Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:   f(x) = ax 2 + bx + c

EJERCICIO : Determinar Dominio y Rango de f(x) = x2 - 2x – 3

Tabulamos valores de los pares ordenados x,y para representarlos en el plano cartesiano;

Ahora ubicamos cada pareja en el plano y unimos los puntos para obtener la gráfica de nuestra función.

Como podemos ver, la gráfica es una parábola. Este tipo de función se conoce como cuadrática y representa a los polinomios de grado 2.

Dominio de la función

Como es una función polinómica de segundo grado el dominio será todo el conjunto de los números reales (siempre tomará valores tanto negativos como positivos en el eje x). 

Dom f(x) = R 

Rango de la función

Note cómo la gráfica empieza a tomar valores en el eje y sólo a partir de un punto determinado. ¨Por lo tanto, en este caso, el rango ya no serán todos los reales. 

Para hallar el Rango, debemos determinar a partir de qué punto la función empieza a tomar valores en el eje y.Esto ocurre en el vértice de la función. 

El vértice  de una función cuadrática se define como (-b /2a, f(-b, 2a)) reemplazando valores tenemos que -b /2a = (-(-2) / 2(1)) = 1.  Este es el valor de x en el vértice.

Ahora reemplazamos este valor de x en la función original para conocer el valor de y en el vértice:

f(1) = 12 - 2(1) – 3 = 1- 2 - 3 = - 4

Por lo tanto, el vértice está en el punto (1, - 4).

El eje “Y” empieza a tomar valores (de abajo hacia arriba) a partir de -4.

Rango = [– 4 , + ∞ )

* El paréntesis cerrado [ o ] significa que el valor está incluido en el intervalo.

* El paréntesis abierto ( o ]) significa que el valor no está incluido en el intervalo.

EJEMPLO 9 :

 Determinar Dominio y Rango de  f(x) = – x2 + 5x - 4

Ahora ubicamos cada pareja en el plano y unimos los puntos para obtener la gráfica de nuestra función.

Dominio de la función

Todos los reales. 

Dom f(x) = R 

Rango de la función

Ahora hallemos el Rango, entonces,  determinemos en qué punto se encuentra el vértice de la función. 

El vértice  está en (-b /2a, f(-b, 2a)) reemplanzando valores tenemos que -b /2a =( - 5 / 2(-1)) = 5/2 (o 2,5).  Este es el valor de x en el vértice.

Ahora reemplazamos este valor de x en la función original para conocer el valor de y en el vértice.

f(5/2) = -(5/2)2 + 5(5/2) – 4 = -25/4 + 25/2 - 4 = 9/4 = 2,25

Por lo tanto, el vértice está en el punto (2.5;  2,25).

El eje “Y” empieza a tomar valores (de abajo hacia arriba) desde menos infinito y llega hasta el vértice de la parábola (hasta Y = 2,25). 

Rango = [– ∞ , 2.25  ) 

EJEMPLO 10 :

* y = −x² + 4x − 3

1. Vértice

x _v = − 4/ −2 = 2     y _v = −2² + 4· 2 − 3 = 1    V(2, 1)

2. Puntos de corte con el eje OX.

x² − 4x + 3 = 0

       (3, 0)      (1, 0)

3. Punto de corte con el eje OY.

(0, −3)

*y = x² + 2x + 1

1. Vértice

x _v = − 2/ 2 = −1     y _v = (−1)² + 2· (−1) + 1= 0     

  V(− 1, 0)

2. Puntos de corte con el eje OX.

x² + 2x + 1= 0

 Coincide con el vértice: (−1, 0)

3. Punto de corte con el eje OY.

 (0, 1)

*y = x² +x + 1

1. Vértice.

x_v = −1/ 2     y_v = (−1/ 2)² + (−1/ 2) + 1= 3/4

V(−1/ 2, 3/ 4)

2. Puntos de corte con el eje OX.

x² + x + 1= 0

1² − 4 < 0       No hay puntos de corte con OX.

3. Punto de corte con el eje OY.

(0, 1)

4.7TÉCNICAS DE GRAFICACION DE FUNCIONES

Desplazamiento vertical de las graficas y = f(x) + k  ( k > 0) y = f(x) - k   ( k > 0)   Observa que la gráfica de y = x2 + 2 sube dos unidades desde el origen y la gráfica de y = x2 - 3 baja tres unidades desde el origen. Nota:  La gráfica de la ecuación de la forma y = f(x) + k es la gráfica de y = f(x) desplazada hacia arriba si k es positiva y desplazada hacia abajo si k es negativa.  De manera que, la gráfica de y = f(x) + k se puede obtener de la gráfica de y = f(x) al trasladar verticalmente la gráfica de y = f(x), k unidades hacia arriba si k es positiva y k unidades hacia abajo si k es negativa. Desplazamiento Horizontal de las Graficas     y = f(x - h)  ( k > 0)  y = f(x + h)  ( k > 0) Observa que la gráfica de y = ( x + 2)2  se mueve dos unidades hacia la izquieda y la gráfica de y = (x - 2)2 se mueve dos unidades hacia la derecha. Nota:  La gráfica de y = f(x + h)  es la gráfica de y = f(x) desplazada hacia la derecha si h es negativa y desplazada hacia la izquierda si h es positiva.  De manera que, la gráfica de y = f( x + h) se puede obtener de la gráfica de y = f(x) al trasladar horizontalmente la gráfica de y = f(x), h unidades hacia la izquierda si h es positiva y h unidades hacia la derecha si h es negativa. EJEMPLO 11 :

4.7 OPERACIONES CON FUNCIONES DE VARIABLE REAL

Sean  f  y  g  dos funciones reales de variable real y de dominios  Dom(f) y Dom(g), respectivamente.

Suma de funciones

Llamamos suma de f y g, a una operación real que denominamos (f + g) tal que:

(f + g) (x) = f(x) + g(x)           , para todo    x ∈ [Dom(f) ∩ Dom(g)]

Llamamos función nula o función cero a aquella función que asigna a cualquier elemento del dominio el valor 0 como imagen. La expresamos por 0.

Se verifica que:

 (f + 0)(x) = f(x) + 0(x) = f(x)

Por tanto, la función nula es el elemento neutro para la suma de funciones.
Dada una función f definida en D, llamamos función opuesta de f, y la expresamos por - f, a la función:







La función opuesta verifica que para toda función f se cumple que:            

              f + (-f) = (-f) + f = 0

La función opuesta es el elemento opuesto para la suma de funciones.

Ejemplos de suma de funciones 12:

Dadas las funciones  f  y  g , vamos a hallar (f + g):

               

Como  Dom(f) = R  y  Dom(g) = R - {1} , tenemos que:

               Dom(f + g) = Dom(f) ∩ Dom(g) = R ∩ [R - {1}] = R - {1}

Veamos si es posible efectuar la suma de estas funciones.

Como  Dom(f) = [9 , ∞)  y  Dom(g) = (-∞ , 5] , tenemos que:

               Dom(f + g) = Dom(f) ∩ Dom(g) = [9 , ∞) ∩ (-∞ , 5] = ∅

No hay ningún elemento que pertenezca a la intersección de los dominios de f y g, por lo que no existe f + g.

Producto de funciones

Llamamos producto de f por g, y lo expresamos por (f · g), a la función:

(f · g)(x) = f(x) · g(x)     , para todo   x ∈ [Dom(f) ∩Dom(g)]

Llamamos función unidad, y la expresamos por 1, a aquella función que a cada número real le asigna el número real 1.

Se verifica que:

               (f · 1)(x) = f(x) · 1(x) = f(x)

La función unidad el elemeno neutro para el producto de funciones.

Dada una función f de dominio D, tal que f(x) ≠ 0 para todo valor x de D, llamamos función recíproca de f, y la expresamos por 1/f, a la función.

La función recíproca es el elemento inverso para el producto de funciones.     

Si f es una función que se anula en algún punto de su dominio D, el dominio de 1/f es:

               Dom(1/f) = D - { x ∈ D / f(x) = 0 }

Ejemplo de producto de funciones 13:

Dadas las funciones  f  y  g , vamos a hallar (f · g):

               

Como  Dom(f) = [3 , ∞)  y  Dom(g) = R - {-2} , tenemos que:

               Dom(f · g) = Dom(f) ∩ Dom(g) = [3 , ∞) ∩ R - {-2} = [3 , ∞)

Ejemplo de función recíproca 14: 

Vamos a hallar la función recíproca de f, donde f es:

Hacemos (1/f)(x):

               

Vemos que:     Dom(f) = R

Y además  f(x) = 0  sólamente si x = 0. Luego:     {x ∈ R / f(x) = 0} = {0}

Por tanto el dominio de la función recíproca de f es:

               

Cociente de funciones

Llamamos cociente de f y g a otra función real que denominamos por f/g, tal que:

Ejemplo de cociente de funciones 15: 

Dadas las funciones  f  y  g , vamos a hallar (f/g):

               

Observamos que  g(x) = 0  sólamente si  x = 5. Luego:     {x / g(x) = 0} = {5}

Como  Dom(f) = [2 , ∞)  y  Dom(g) = R - {-3} , tenemos que:

               Dom(f / g) = [Dom(f) ∩ Dom(g)] - {x / g(x) = 0} = [ [2 , ∞) ∩ R - {-3} ] - {5} = [2 , ∞) - {5}

4.8 FUNCIONES POLINOMIALES

Una función polinómica es aquella que está definida por un polinomio:

donde   a₀, a₁ ... a_n-1, a_n   son números reales que se llaman coeficientes del polinomioy   n   es el grado del polinomio.

Las características generales de las funciones polinómicas son las siguientes:

1) El dominio de definición es el conjunto de los números reales (R).

2) Son siempre continuas.

3) No tienen asíntotas.

4) Cortan al eje X, como máximo, un número de veces igual que el grado del polinomio.

5) Cortan el eje Y en el punto (0, a₀).

6) El número de máximos y mínimos relativos es, a lo sumo, igual al grado del polinomio menos uno.

7) El número de puntos de inflexión es, a lo sumo, igual al grado del polinomio menos dos.

Funciones polinómicas de grado 0: 

rectas horizontales

Funciones polinómicas de segundo grado:   

 parábolas

Funciones polinómicas de tercer grado:    cúbicas

Funciones polinómicas de cuarto grado:  cuárticas

4.9 FUNCIONES RACIONALES

Una función es racional si es el cociente de dos polinomios:

siendo el grado del polinomio   Q(x)   distinto de 0.

Las características generales de las funciones racionales son:

1) El dominio de las funciones racionales son los números reales menos las raíces del denominador, es decir: 

2) Son discontinuas en los valores de   x   que son raíces del denominador.

3) Tienen asíntotas verticales en cada raíz del denominador que no lo sea del numerador, y pueden tener asíntotas horizontales y oblicuas.

Función de proporcionalidad invers

Una función de proporcionalidad inversa es una función racional del tipo:

Su gráfica es una hipérbola.

Las características generales de las funciones de proporcionalidad inversa son:

1) El dominio de la función de proporcionalidad inversa es   R - {0} .

2) La función es discontinua en   x = 0

3) En   x = 0    existe una asíntota vertical.

4) A medida que los valores de   x   crecen o decrecen, la función se acerca al eje Y, por lo tanto tiene una asíntota horizontal en   y = 0 .

5) La gráfica de este tipo de funciones no corta a los ejes de coordenadas.

6) La función es impar y por tanto simétrica al origen de coordenadas.

7) Para   k > 0   la función es decreciente y la gráfica está en el primer y tercer cuadrante.

Para   k < 0   la función es creciente y la gráfica está en el segundo y cuarto cuadrante.

EJEMPLO: 16

Representación gráfica de funciones de proporcionalidad inversa:

1) Puntos de corte con los ejes:

Para   x = 0   la función   f(x)   no está definida puesto que    f(0) = 3/0 (no real).

Para   x = 0   la función   g(x)   no está definida puesto que    g(0) = - 3/0 (no real).

2) Simetrías:

Las funciones   f(x)   y   g(x)   son impares, es decir, son simétricas respecto al eje de coordenadas.

     

   

3) Crecimiento o decrecimiento:

Para la función   f(x)   tenemos que   k > 0 ,  por lo tanto la función es decreciente y la gráfica está en el primer y tercer cuadrante. Es decir, la función es decreciente en   (- ∞, 0) ∪ (0, + ∞).

Para la función   g(x)   tenemos que   k < 0 ,  por lo tanto la función es creciente y la gráfica está en el segundo y cuarto cuadrante. Es decir, la función es creciente en   (- ∞, 0) ∪ (0, + ∞).

4) Tabla de valores:

Construimos una tabla de valores.

EJEMPLOS DE GRAFICAS

4.10 FUNCIONES EXPONENCIALES

Además de funciones lineales, cuadráticas, racionales y radicales, existen las funciones exponenciales. Las funciones exponenciales tienen la forma f(x) = b^x, donde b > 0 y b ≠ 1. Al igual que cualquier expresión exponencial, b se llama base y x se llama exponente.

Un ejemplo de una función exponencial es el crecimiento de las bacterias. Algunas bacterias se duplican cada hora. Si comienzas con 1 bacteria y se duplica en cada hora, tendrás 2^x bacterias después de x horas. Esto se puede escribir como f(x) = 2^x.

Antes de empezar,   f(0) = 2⁰ = 1

Después de 1 hora   f(1) = 2¹ = 2

Después de 2 horas f(2) = 2² = 4

En 3 horas                f(3) = 2³ = 8

etc.

Con la definición f(x) = b^x y las restricciones de b > 0 y b ≠ 1, el dominio de la función exponencial es el conjunto de todos los números reales. El rango es el conjunto de todos los números reales positivos. La siguiente gráfica muestra f(x) = 2^x.

Crecimiento exponencial

Como pudiste ver arriba, esta función exponencial tiene una gráfica que se acerca mucho al eje x porque se extiende a la izquierda (conforme x se vuelve más negativa), pero nunca toca el eje x. Conocer la forma general de las funciones exponenciales es útil para graficar ecuaciones o funciones exponenciales específicas.

Hacer una tabla de valores también es útil, porque puedes usar la tabla para encontrar la curva de la gráfica con más precisión. Algo que recordar es que la base tiene un exponente negativo, entonces tomas el recíproco de la base para hacer el exponente positivo. Por ejemplo, .

Ejemplo
Problema	Hacer una tabla de valores para f(x) = 3x.
	x f(x)	Has una “T” para empezar la tabla con dos columnas. Etiqueta las columnas con x y f(x).
	x f(x) −2 −1 0 1 2	Escoge varios valores para x y ponlos como filas separadas en la columna x. Consejo: Siempre es bueno incluir el 0, valores positivos y valores negativos, si es posible.
Respuesta	x f(x) −2 −1 0 1 1 3 2 9	Evalúa la función para cada valor de x y escribe el resultado en la columna f(x) junto al valor de xcorrespondiente. Por ejemplo, cuando x = −2, f(x) = 3-2 =  = , entonces  va en la columna f(x) junto al −2 de la columna x. f(1) = 31 = 3 y 3 va en la columna f(x) junto al 1 de la columna x. Observa que tu tabla de valores podría ser distinta a la de alguien más, si escogiste diferentes números para x.

Observa la tabla de valores. Piensa en lo que pasa conforme los valores de x aumentan — ¡también aumenta los valores de la función (f(x) o y)!

Ahora que tienes la tabla de valores, puedes usarlos para dibujar la forma y la posición de la función. Conecta los puntos lo mejor que puedas para hacer una curva suave (no una serie de líneas rectas). Esto muestra que todos los puntos en la curva son parte de esta función.

Ejemplo
Problema	Graficar f(x) = 3x.
	x f(x) −2 −1 0 1 1 3 2 9	Empieza con una tabla de valores, como la que hiciste en el ejemplo anterior.
	x f(x) punto −2 (−2, ) −1 (−1, ) 0 1 (0, 1) 1 3 (1, 3) 2 9 (2, 9)	Si piensas en f(x) como y, cada fila forma un par ordenado que puedes graficar en las coordenadas.
		Grafica los puntos.
Respuesta		Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas). Usa la forma de una gráfica exponencial para ayudarte: esta gráfica se acerca mucho al eje x en la izquierda, pero nunca lo toca y se vuelve más inclinada a la derecha.

Este es un ejemplo de un crecimiento exponencial. Conforme aumenta x, f(x) “crece” más rápido. Intentemos otro.

Ejemplo
Problema	Graficar f(x) = 4x.
	x f(x) −2 −1 0 1 1 4 2 16	Empieza con una tabla de valores. Puedes escoger diferentes valores pero de nuevo, es útil incluir el 0 y algunos valores positivos y negativos.. Recuerda, 4-2 =  = . Si piensas en f(x) como y, cada fila forma un par ordenado que puedes graficar en las coordenadas.
		Grafica los puntos. Observa que la base más grande en este problema hizo que el valor de la función se disparara. Incluso con un valor pequeño de 2 para x, el valor de la función es tan grande que se sale de la escala que usaste antes. Puedes cambiar la escala, pero entonces los valores quedan muy juntos uno con otro. También puedes intentar con otros puntos, como cuando x =. Porque conoces la raíz cuadrada de 4, puedes encontrar el valor en este caso: . El punto  es el punto azul en la gráfica. Para otras bases, podrías necesitar una calculadora para ayudarte a encontrar el valor de la función.
Respuesta		Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas). Usa la forma de una gráfica exponencial para ayudarte: esta gráfica se acerca mucho al eje x en la izquierda, pero nunca lo toca y se vuelve más inclinada a la derecha.

Comparemos las tres gráficas que hemos visto. Las funciones f(x) = 2^x, f(x) = 3^x y

f(x) = 4^x están graficadas a continuación.

Observa que una base más grande hace más empinada la gráfica. Una base más grande también hace que la gráfica se acerque al eje y por x > 0 y más cerca al eje x por x < 0. ¡Todas las gráficas pasan por (0, 1)!

Decaimiento exponencial

Recuerda que para las funciones exponenciales, b > 0, pero b ≠ 1. En los ejemplos anteriores, b > 1. ¿Qué pasa cuando b está entre 0 y 1, 0 < b < 1?

Ejemplo
Problema	Graficar .
	x f(x) −2 4 −1 2 0 1 1 2	Empieza con una tabla de valores. ¡Ten cuidado con los exponentes negativos! Recuerda sacar el recíproco de la base para volver positivo el exponente. En este caso,  y .
		Usa la tabla como pares ordenados y grafíca los puntos.
Respuesta		Como los puntos no están en una línea, no puedes usar una regla. Conecta los puntos lo mejor que puedas usando una curva suave (no una serie de líneas rectas).

4.11 FUNCIONES LOGARITMICAS

Las funciones logarítmicas son funciones del tipo:

Es la inversa de la función exponencial   f(x) = a^x

Las características generales de las funciones logarítmicas son:

1) El dominio de una función logarítmica son los números reales positivos:    Dom(f) = (0. + ∞) .

2) Su recorrido es R:    Im(f) = R .

3) Son funciones continuas.

4) Como   log_a1 = 0 , la función siempre pasa por el punto   (1, 0) .

 La función corta el eje X en el punto   (1, 0)   y no corta el eje Y.

5) Como   log_aa = 1 , la función siempre pasa por el punto   (a, 1) .

6) Si   a > 1   la función es creciente.

   Si   0 < a < 1   la función es decreciente.

7) Son convexas si   a > 1 

   Son concavas si   0 < a < 1 .

8) El eje Y es una asíntota vertical.

1. Si  a > 1 : 
2. Cuando x → 0 ⁺ , entonces log _a x → - ∞
3. Si  0 < a < 1 :
4. Cuando x → 0 ⁺ , entonces log _a x → + ∞

EJEMPLO 17:

1) Dominio:

El dominio de las funciones logarítmicas es   (0, + ∞) .

Dom(f) = Dom(g) = (0, + ∞) .

2) Recorrido:

El recorrido de las funciones logarítmicas es R.

Im(f) = Im(g) = R .

3) Puntos de corte:

f(1) = log₂1 = 0  ,   el punto de corte con el eje X es   (1, 0).

g(1) = log_1/21 = 0  ,   el punto de corte con el eje X es   (1, 0).

La funciones   f(x)   y   g(x)   no cortan al eje Y.

3) Crecimiento y decrecimiento:

La función   f(x)   es creciente ya que   a > 1 .

La función   g(x)   es decreciente ya que   0 < a < 1 .

4) Concavidad y convexidad:

Las función   f(x)    es convexa ya que   a > 1 .

Las función   g(x)   es concava ya que   0 < a < 1 .

5) Asíntotas:

Las funciones   f(x)   y   g(x)   tienen una asintota en el eje Y.

6) Tabla de valores:

PROPIEDADES 

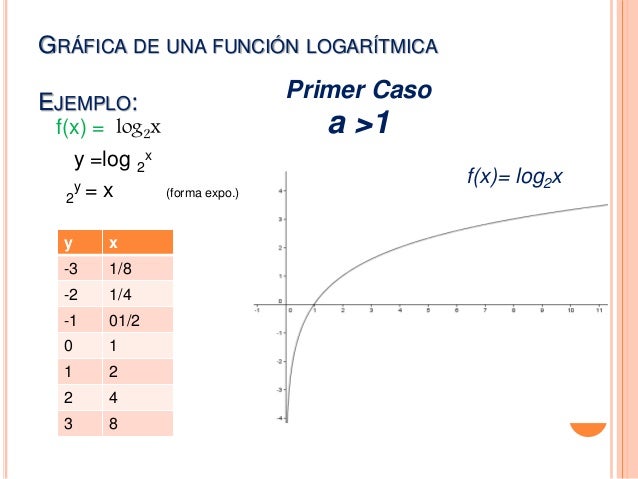
GRÁFICAS DE FUNCIONES LOGARÍTMICAS

EJEMPLO 18: