¿Qué es un punto?
El punto es el elemento base de la geometría, ente fundamental, porque con él determinamos las rectas y los planos. Podemos definirlo también, como la intercesión de dos líneas. Sirve para indicar una posición y no tiene dimensión.
¿Qué es una recta?
Una recta es una sucesión ininterrumpida de puntos con una misma dirección, por lo tanto sólo tiene una dimensión. Dos puntos determinan una recta la recta es infinita, no posee ni principio ni fin.
Una recta es una sucesión ininterrumpida de puntos con una misma dirección, por lo tanto sólo tiene una dimensión. Dos puntos determinan una recta la recta es infinita, no posee ni principio ni fin.
Tipos de rectas
- Recta: La recta propiamente dicha se caracteriza porque los puntos que la forman están en la misma dirección. Tiene una sola dirección y dos sentidos. No se puede medir.
- Semirrecta: Es línea recta que tiene origen pero no tiene fin, tiene sólo un sentido, y no se puede medir.
- Segmento: Un segmento es una línea recta que tiene principio y fin, un segmento se puede medir.
- Poligonal: Se llama recta poligonal aquella que está formada por varias porciones de rectas que están unas a continuación de otras, pero no están alineadas, la línea poligonal puede ser abierta (cuando ningún extremo se une) o cerrada (cuando el primer extremo se une con el último). La línea poligonal cerrada forma una figura plana que se llama polígono.
- Curva:Una curva está formada por puntos que están en distinta dirección. Puede ser curva abierta (los externos no se unen) curva cerrada (cuyos extremos se unen) y curva mixta (formada por lineas rectas y curvas unidas)
Posiciones de las rectas:
- Dos rectas son paralelas: si no tienen ningún punto en común.
- Dos rectas son secantes: cuando tienen un punto en común.
- Dos rectas son perpendiculares: cuando al cortarse forman cuatro ángulos rectos.
Posición de las rectas en el espacio
- Horizontal
- Vertical
- Inclinada
La linea curva puede ser:
- Circunferencia, es una curva regular cerrada, cuyos puntos están todos a la misma distancia de otro llamado centro.
- Elípse, es una curva regular cerrada que se diferencia de la anterior porque la suma de la distancia de cada uno de sus puntos respecto a otros dos que están en su interior es siempre igual.
- Espiral es una curva regular abierta que gira sobre sí misma.
- Parábola es una curva regular abierta, cada uno de sus puntos está a una distancia siempre igual de un punto fijo llamado foco y de una recta llamada directriz.
ECUACION DE LA RECTA
La ecuación de una recta es de la forma
EJEMPLO 1:
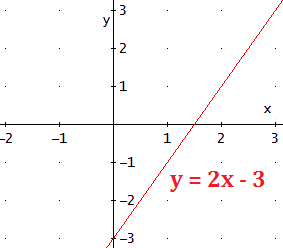
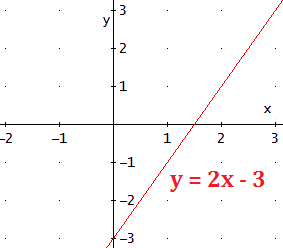
Al número a se le llama pendiente y a al número b, término independiente u ordenada al origen.
Puntos de corte de una Recta
Puntos de corte o intersección con los ejes:
Con el eje OY (de ordenadas)
Ocurre cuando x = 0. Sustituimos x por 0 en la ecuación y obtenemos el valor de y. Es decir, y = b. El punto es (0, b).
Ejemplo:
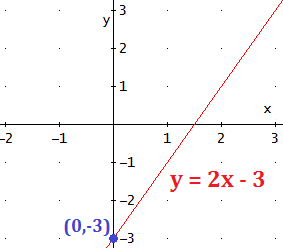
Ocurre cuando x = 0. Sustituimos x por 0 en la ecuación y obtenemos el valor de y. Es decir, y = b. El punto es (0, b).
Ejemplo:
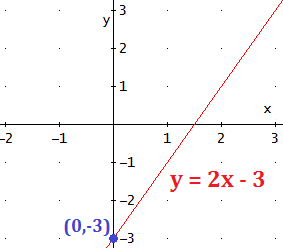
Con el eje OX (de abscisas):
Ocurre cuando y = 0. Sustituimos y por 0 en la ecuación y calculamos x. Es decir,
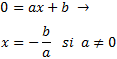 El punto es (-b/a,0).
El punto es (-b/a,0).
Ejemplos:
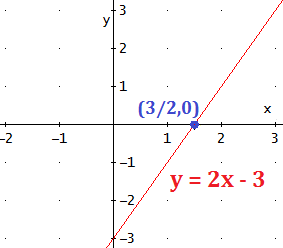
Ocurre cuando y = 0. Sustituimos y por 0 en la ecuación y calculamos x. Es decir,
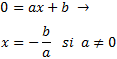
Ejemplos:
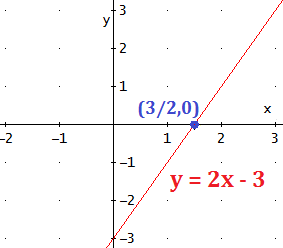
Rectas especiales
Hay dos casos particulares de rectas: las verticales y las horizontales.
Recta horizontal:
Son las rectas que no tienen pendiente, es decir, es una recta paralela al eje OX.
Son de la forma
EJEMPLO 2:
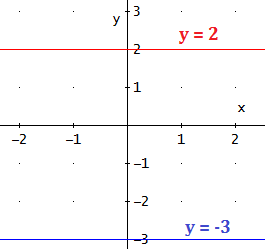
Son las rectas que no tienen pendiente, es decir, es una recta paralela al eje OX.
Son de la forma
Esta recta corta al eje OY en el punto (0,k) y si k = 0, entonces la recta coincide con el eje OX.
EJEMPLO 2:
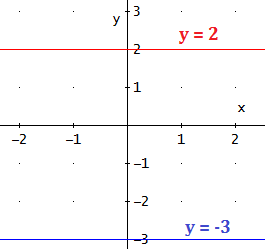
Recta vertical:
Son rectas paralelas al eje de ordenadas (eje OY).
Son de la forma
EJEMPLO 3:
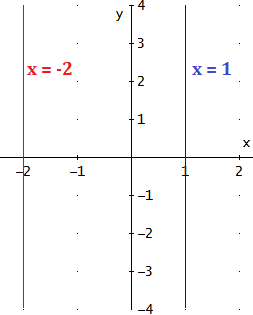
Son rectas paralelas al eje de ordenadas (eje OY).
Son de la forma
Esta recta corta el eje OX en el punto (k,0) y si k = 0, entonces la recta coincide con el eje OY.
EJEMPLO 3:
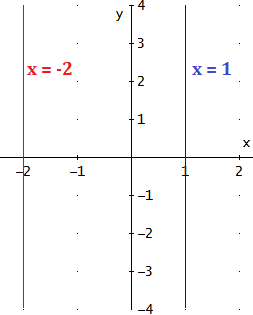
EJEMPLO 4 :
Hallar la ecuaci�n de la recta que pasa por el punto (1, 2) y tiene pendiente m = - 5.
Tienes que hallar la ecuaci�n de la recta, esto es, y = mx + b.
Usa la informaci�n que te dan: m = - 5 y sustituye en la ecuaci�n:
y = - 5x + b
Ahora tienes que buscar la b; usa el otro dato; la recta pasa por el punto (1, 2), por lo tanto, ese punto es una soluci�n de la ecuaci�n que estas buscando. Sustituye esos valores de x = 1, y = 2 en la ecuaci�n que estas buscando: 2 = - 5 ( 1 ) + b
Despeja la variable b en:
2 = - 5 ( 1 ) + b
2 = - 5 + b
2 + 5 = b
b = 7
Sustituye el valor de b en la ecuaci�n que estas buscando: y = - 5x + 7
La ecuaci�n es y = - 5x + 7.
EJEMPLO 5 :
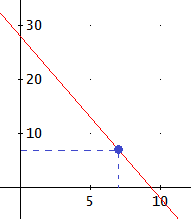
Calcular la recta que pasa por el punto A( 7,7) y que tiene pendiente -3. ¿Pasa también por el origen? El origen es el punto O(0,0).
La ecuación de la recta será de la forma
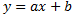 como la pendiente tiene que ser -3, tenemos que a = -3.
como la pendiente tiene que ser -3, tenemos que a = -3.
Puesto que la recta pasa por el punto A, sus coordenadas verifican la ecuación. Sustituyendo en la ecuación obtenemos b:
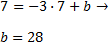 Por tanto, la ecuación de la recta es
Por tanto, la ecuación de la recta es
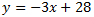 Si la recta pasa por el origen, sus coordenadas verifican la ecuación. Es decir, para x = 0tenemos que obtener y = 0, pero obtenemos
Si la recta pasa por el origen, sus coordenadas verifican la ecuación. Es decir, para x = 0tenemos que obtener y = 0, pero obtenemos
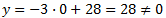 Así que la recta no pasa por el origen.
Así que la recta no pasa por el origen.
La gráfica de la recta es
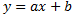
Puesto que la recta pasa por el punto A, sus coordenadas verifican la ecuación. Sustituyendo en la ecuación obtenemos b:
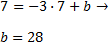
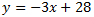
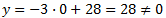
La gráfica de la recta es

Para lograrlo debemos conocer dos elementos importantes:
- el centro de la circunferencia (C), dado por sus coordenadas
- el radio (r) de la misma circunferencia
Definido esto, tendremos dos posibilidades :
A) Circunferencia con centro (C) en el origen de las coordenadas; expresado como C (0, 0)
B) Y circunferencia con centro (C) fuera del origen de las coordenadas; expresado, por ejemplo, como C (3, 2) .
A continuación analizaremos cuatro casos
Caso 1
Veamos la gráfica siguiente:

Los datos que nos entrega son:
Centro: C (0, 0) , el centro se ubica en el origen de las coordenadas x e y
radio: r = 3 , lo indica el 3 en cada una de las coordenadas.
Recordar esto:
Cuando el centro (C) de la circunferencia sea (0, 0) se usará la ecuación x 2 + y 2 = r 2 para expresar dicha circunferencia en forma analítica ( Geometría analítica ) . Esta ecuación se conoce como ecuación reducida .
Para la gráfica de nuestro ejemplo, reemplazamos el valor de r en la fórmula x 2 + y 2 = 3 2
y nos queda x 2 + y 2 = 9 como la ecuación reducida de la circunferencia graficada arriba.
y nos queda x 2 + y 2 = 9 como la ecuación reducida de la circunferencia graficada arriba.
Ojo:
Si nos dieran la ecuación x 2 + y 2 = 9 y nos preguntaran qué representa, razonamos en sentido inverso y diremos que representa una circunferencia, con centro (C) en el origen de las coordenadas (0, 0) y cuyo radio es 3 (3 2 = 9 y la raíz cuadrada de 9 es 3)
|
Caso 2
Veamos la gráfica siguiente:
Los datos que nos entrega son:
Centro: C (0, 0) , el centro se ubica en el origen de las coordenadas x e y
radio: r , lo desconocemos, pero tenemos un dato: el punto P (3, 4) ubicado en la circunferencia.
Cuando el centro (C) de la circunferencia sea (0, 0) se usará la ecuación x 2 + y 2 = r 2 para expresar dicha circunferencia en forma analítica. Esta ecuación se conoce como ecuación reducida .
Para la gráfica de nuestro ejemplo, deberíamos colocar el valor de r en la fórmula x 2 + y 2 = r 2 , pero resulta que no lo conocemos.
Entonces, a partir del dato P (3, 4) podemos calcular el valor del trazo que une este punto con el centro C (0, 0) (trazo PC con línea punteada en la figura), el cual corresponde al radio de la circunferencia dada.
¿Cómo calculamos el valor de la distancia (d) entre P y C (el radio de la circunferencia)?
Para calcular la distancia (d) entre dos puntos (encontrar su valor) contamos con la siguiente fórmula:
No olvidemos que esta fórmula es para encontrar o conocer la distancia entre dos puntos ; por lo mismo, debemos saber que en ella
(x 2 ─ x 1 ) 2 representa al punto 1, y ese punto 1 (P 1 ) lo haremos corresponder con el punto que pasa por el centro C (0, 0)
(y 2 ─ y 1 ) 2 representa al punto 2, y ese punto 2 (P 2 ) lo haremos corresponder con el punto que pasa por P (3, 4).
Es muy importante conocer o designar este orden ya que
Establecido este orden o equivalencia, podemos sustituir los valores en la fórmula anterior para conocer la distancia (d) entre los dos puntos que nos interesan, la cual será nuestro radio:
El 5 nos indica la distancia entre los dos puntos, el centro de la circunferencia y uno de sus puntos, lo cual corresponde al radio .
Recordemos de nuevo :
Cuando el centro (C) de la circunferencia sea (0, 0) se usará la ecuación x 2 + y 2 = r 2 para expresar dicha circunferencia en forma analítica. Esta ecuación se conoce como ecuación reducida .
Para la gráfica de nuestro ejemplo, deberíamos colocar el valor de r en la fórmula x 2 + y 2 = r 2 , pero resulta que no lo conocemos.
Pero tenemos identificados dos puntos opuestos en la circunferencia, los cuales unidos entre sí (la línea punteada entre A y B en la gráfica) representan al diámetro de la misma. Entonces, a partir de esos puntos, A (-3, -2) y B (3, 2), podemos calcular el valor del trazo que los une (trazo AB con línea punteada en la figura), el cual corresponde al diámetro de la circunferencia dada.
¿Cómo calculamos el valor de la distancia (d) entre A y B (el diámetro de la circunferencia)?
Para calcular la distancia (d) entre dos puntos (encontrar su valor) contamos con la siguiente fórmula:
No olvidemos que esta fórmula es para encontrar o conocer la distancia entre dos puntos; por lo mismo, debemos saber que en ella
(x 2 ─ x 1 ) 2 representa al punto 1, y ese punto 1 (P 1 ) lo haremos corresponder con el punto A (-3, -2)
(y 2 ─ y 1 ) 2 representa al punto 2, y ese punto 2 (P 2 ) lo haremos corresponder con el punto B (3, 2).
Es muy importante conocer o designar este orden ya que
Establecido este orden o equivalencia, podemos sustituir los valores en la fórmula anterior para conocer la distancia (d) entre los dos puntos que nos interesan, la cual será nuestro diámetro
El 7,2 (valor aproximado) nos indica la distancia entre los dos puntos, A y B, la cual corresponde al diámetro de la circunferencia.
Para conocer el valor del radio, simplemente dividimos por 2 dicho diámetro, y nos queda r = 3,6 ≈
Para conocer el valor del radio, simplemente dividimos por 2 dicho diámetro, y nos queda r = 3,6 ≈
Conocido el radio lo reemplazaremos en la ecuación de la circunferencia cuyo centro está en el origen de las coordenadas, que es:
x 2 + y 2 = r 2
la cual nos queda
x 2 + y 2 = (3,6) 2 .
x 2 + y 2 = 13 ≈ como la ecuación reducida de la circunferencia graficada arriba (en la cual nos indicaron un centro y dos puntos opuestos en ella).
Esta ecuación también podía obtenerse haciendo el cálculo para la distancia entre uno de los puntos dados y el centro, como se vio en el caso 2
Ojo:
Si nos dieran la ecuación x 2 + y 2 = 13 y nos preguntaran qué representa, razonamos en sentido inverso y diremos que representa una circunferencia, con centro (C) en el origen de las coordenadas (0, 0) y cuyo radio es 3,6 (3,6) 2 = 13 y la raíz cuadrada de 13 es 3,6 ≈).
|
Caso 4
Tenemos la gráfica de una circunferencia con centro (C) en el origen de las coordenadas (0, 0), no hay otro dato sobre coordenadas, pero se me indica que tiene un área de 10 u 2 (diez unidades cuadráticas).
La ecuación general de una parábola es
los coeficientes b y c pueden ser 0. Si a = 0, es una recta y no una parábola.
- Cuando a > 0, la parábola tiene forma de U.
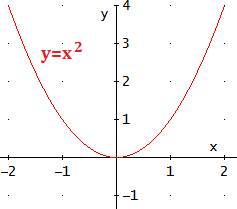
- Cuando a < 0, tiene forma de U invertida.
Puntos de corte
Con el eje OY (de ordenadas):
Ocurre cuando x = 0. Es decir, y = c. El punto es (0,c).
EJEMPLO 6:
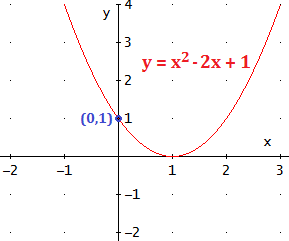
Ocurre cuando x = 0. Es decir, y = c. El punto es (0,c).
EJEMPLO 6:

Con el eje OX (de abscisas):
Ocurre cuando y = 0. Es decir,
EJEMPLO 7:
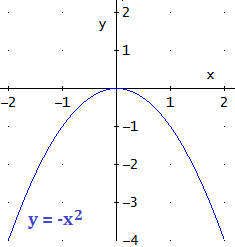
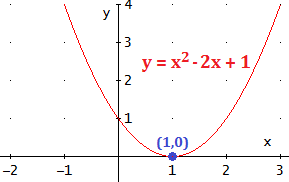
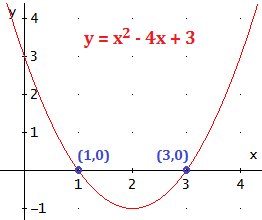
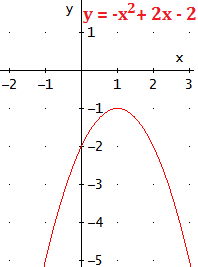
La parábola y = x2 - 2x + 1 tiene sólo un punto de corte con el eje de abscisas ya que la ecuación sólo tiene una solución:
Vértice
El vértice de una parábola es su punto máximo o mínimo (uno de los dos). Es el máximo si la parábola tiene forma de U invertida y es el mínimo si tiene forma de U.
EJEMPLO 8:
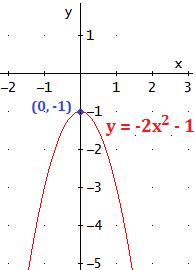 El vértice de la parábola y = -2x2 - 1 es un máximo.
El vértice de la parábola y = -2x2 - 1 es un máximo.
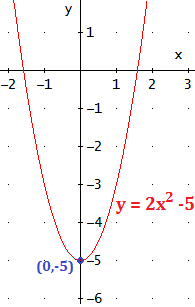 El vértice de la parábola y = 2x2 - 5 es un mínimo.
El vértice de la parábola y = 2x2 - 5 es un mínimo.
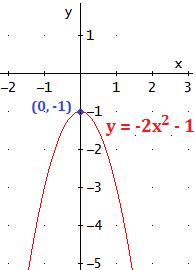
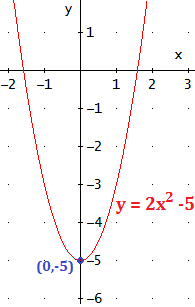
El vértice está en el punto cuya primera coordenada es
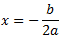
Para saber la coordenada y tenemos que substituir en la ecuación el valor de x.
EJEMPLO 9 : Calcular los puntos de corte de la siguiente parábola con los ejes de coordenadas:
problemas resueltos de parábolas
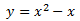
Podemos escribir la ecuación en forma factorizada como
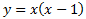
Puntos de corte con el eje de abscisa (eje OX): ocurre cuando y=0. Sustituimos en la ecuación y obtenemos
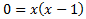
Y como la ecuación de segundo grado está factorizada no es necesario aplicar la fórmula cuadrática. Las soluciones son x=0,1.
Luego tenemos dos puntos de corte
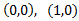
Punto de corte con el eje de ordenadas (eje OY): ocurre cuando x=0. Sustituimos en la ecuación y obtenemos
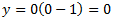
El punto es (0,0).
Notemos que hemos obtenido el punto (0,0) (el origen) como punto de corte con el eje de abscisas y el de ordenadas. Y es que, en efecto, en el origen, la parábola corta a los dos ejes.
Calculamos ahora el vértice y con los puntos de corte y el vértice podemos graficar rápidamente la parábola:
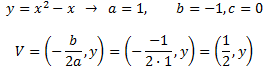
El valor de y lo obtenemos sustituyendo el valor de x en la ecuación:
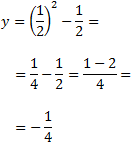
El vértice es
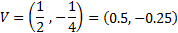
La gráfica es
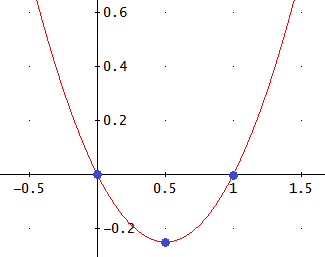
Encontrar las dos parábolas que cortan al eje de abscisas (eje OX) en los puntos A(0,0), B(2,0) pero con vértices distintos (1,-5) y (1,-2).
La ecuación general de una parábola
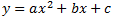 Sabemos que las dos rectas pasan por los puntos
Sabemos que las dos rectas pasan por los puntos
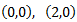 Luego dichos punto verifican la ecuación. Los sustituimos en:
Luego dichos punto verifican la ecuación. Los sustituimos en:
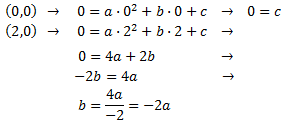 Por tanto, ya sabemos que ambas parábolas son la ecuación
Por tanto, ya sabemos que ambas parábolas son la ecuación
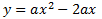 El valor de a lo obtendremos a partir del vértice, que sabemos que son
El valor de a lo obtendremos a partir del vértice, que sabemos que son
 Sustituimos en la ecuación:
Sustituimos en la ecuación:
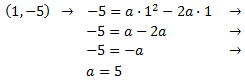 Por tanto, una de las parábolas es
Por tanto, una de las parábolas es
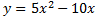 Del otro vértice obtenemos
Del otro vértice obtenemos
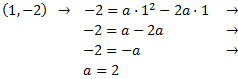 Luego la otra parábola es
Luego la otra parábola es
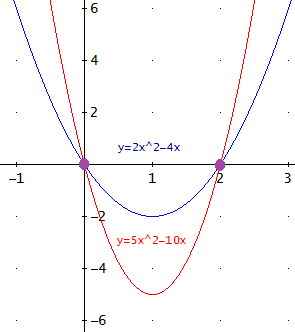
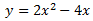 Con los 3 puntos de cada parábola podemos graficarlas rápidamente
Con los 3 puntos de cada parábola podemos graficarlas rápidamente
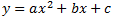
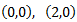
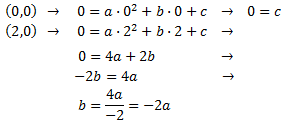
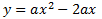

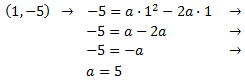
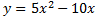
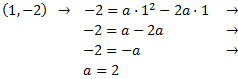
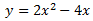

10.4 ELIPSE
La elipse es el lugar geométrico de los puntos del plano cuya suma de las distancias a los dos focos (puntos interiores fijos F1 y F2) es constante. Es decir, para todo punto a de la elipse, la suma de las distancias d1 y d2 es constante.
También podemos definir la elipse como una cónica, consecuencia de la intersección de un cono con un plano oblicuo que no corta la base.
Elementos de una elipse
Los elementos más importante de la elipse son:
- Focos: son los puntos fijos F1 y F2 que generan la elipse. La suma de las dos distancias de cualquier punto de la elipse a los dos focos (d1 y d2) es constante.
- Distancia focal (2c): distancia entre los dos focos. F1F2=2c. c es la semidistancia focal.
- Centro: es el punto medio de los dos focos (O).
- Semieje mayor: longitud del segmento OI o OK (a). La longitud es mayor (o igual en el caso de la circunferencia) a la del semieje menor. La suma de las distancias de cualquier punto de la elipse a los focos es constante y ésta es igual a dos veces el semieje mayor:
- Semieje menor: longitud del segmento OJ o OL (b). Ambos semiejes son los dos ejes de simetría de la elipse. Se cumple que:Como vemos en el dibujo, esta relación cumple el teorema de Pitágoras.
- Radios vectores: los radios vectores de cualquier punto de la elipse (P=(x,y)) son los dos segmentos que lo unen con los dos focos. PF1 y PF2 (en el dibujo, d1 y d2).
- Vértices: son los puntos resultantes de la intersección de la elipse con la recta que pasa por los focos, F1F2, y su perpendicular que pasa por el centro. Es decir, son los puntos I, J, K y L
Ecuación de una elipse
Los puntos pertenecientes a la elipse (x,y) son los puntos del plano que cumplen que la suma de su distancia a los dos focos es constante. La ecuación de la elipse es la siguiente:
En el caso de que la elipse esté centrada (el centro es el punto (0,0)), la ecuación es:
Área de una elipse
El área comprendida dentro de una elipse es π veces el producto de los dos semiejes (a y b).
En el caso de que los dos semiejes sean iguales (r=a=b), su fórmula es la misma que el área comprendida dentro de una circunferencia (o lo que es lo mismo, el área del círculo):
Perímetro de una elipse
El cálculo del perímetro de la elipse (o longitud de la elipse) es muy difícil, aunque no lo parezca. Requiere de integrales complicadas para su cálculo. Existen fórmulas que aproximan el cálculo hasta valores bastante exactos. Existe una aproximación con menos del 5% de error, siempre que el semieje mayor (a) no sea mucho más grande que el menor (b):
El matemático Ramanujan dio una aproximación más exacta que la anterior :
Excentricidad de la elipse
La excentricidad de una elipse (e) es un valor que determina la forma de la elipse, en el sentido de si es más redondeada o si se aproxima a un segmento. Sea c la semidistancia focal y a el semieje mayor:
La excentricidad puede tomar valores entre 0 y 1 (0≤e≤1). Es 0 cuando la elipse es una circunferencia. En este caso los semiejes mayor y menor son iguales y los focos (F1 y F1) coinciden en el centro de la elipse. Cuando la excentricidad crece y tiende a 1, la elipse se aproxima a un segmento.
Existe otra fórmula que calcula la excentricidad a partir de los dos semiejes (a y b).
No hay comentarios.:
Publicar un comentario