7. GEOMETRÍA PLANA

7.1 FIGURAS GEOMÉTRICAS EN EL PLANO 

EJEMPLO1.

El área de un triángulo de vértices A(x₁, y₁, z₁) , B(x₂, y₂, z₂) y C(x₃, y₃, z₃) es :

EJEMPLO 2:

ÁREA DEL CUADRADO
La fórmula del área del cuadrado es
ÁREA= lado·lado=l² Nos da las unidades cuadradas, es decir los cuadrados de lado 1, que caben dentro de nuestro cuadrado ABCD. La siguiente ventana te ayudará a comprobar esta fórmula. Con  el botón puedes cambiar la longitud del lado.

ÁREA DEL RECTÁNGULO
La fórmula del área del rectángulo es
AREA= lado·lado=a·b Nos da las unidades cuadradas del rectángulo ABCD, como puedes ver en la siguiente ventana. Ahora con los botones puedes cambiar las longitudes de los dos lados.

Si dejas fijo el lado  a, por ejemplo con el valor 3 verás que los valores del área al ir cambiando b son los de la tabla de multiplicar del 3, ¿puedes explicar por qué? ¡El área del rectángulo era la interpretación geométrica que los griegos usaban para la multiplicación!

ÁREA DEL PARALELOGRAMO
La fórmula del área del paralelogramo es
AREA= base·altura=b·h Para demostrar esta fórmula vamos ver que el paralelogramo ABCD tiene la misma área que la de un rectángulo que tiene lados b y h. Como ya conocemos la fórmula del área del rectángulo podremos concluir que el área del paralelogramo es b·h. En la siguiente ventana se describen los pasos de la demostración. Intenta entender todos los pasos hasta que seas capaz de hacerla tú mismo con lápiz y papel.

ÁREA DEL TRIANGULO 
Con ayuda de las siguientes ventanas vamos a deducir la fórmula para calcular el área del triángulo:
Nos ayudaremos de una técnica que usamos mucho en esta unidad : obtener una fórmula  (que no conocemos) a partir de la fórmula de otra figura que ya conocemos. En este caso, obtendremos la fórmula del triángulo a partir de la del paralelogramo. Recuerda, que a su vez dedujimos la del paralelogramo a partir de la del rectángulo.
Antes de considerar el caso más general, en la siguiente ventana se muestra como obtener la fórmula del área de un triángulo a partir de la de un rectángulo. En la figura puedes comprobar que dividimos el triángulo ABC en dos triángulos mediante la altura h, si pulsas el botón "mostrar"  podrás comprobar que a cada triángulo le corresponde otro triángulo más oscuro  de  igual tamaño. Vemos que el área del rectángulo es por lo tanto dos veces el área del triángulo, como conocemos la fórmula para el rectángulo basta dividirla por dos.

ÁREA DEL ROMBO 
El rombo es un caso especial de paralelogramo en que los cuatro lados son iguales. Si conociésemos la base y la altura podríamos usar la fórmula  para el área de un paralelogramo. Es más frecuente, sin embargo, expresar el área del rombo en función de sus diagonales. La fórmula del área del rombo en función de las diagonales es:
En la figura puedes ver que hemos llamado a y b a las diagonales, también hemos construido un rectángulo alrededor de nuestro rombo; vamos a deducir la fórmula del área del rombo a partir de la del rectángulo. Si pulsas el botón verás que aparecen cuatro triángulos verdes que son iguales a los cuatro triángulos que forman el rombo, por lo tanto tenemos que el área del rombo es la mitad de la del rectángulo.

EJEMPLO 3:


EJEMPLO 4 :



7.2 CLASES DE RECTA EN EL PLANO

RECTAS SECANTES

Las rectas secantes se cortan en un punto.

Son las que situadas en un plano se cortan en un punto.

Las rectas A y B de la siguiente figura se cortan en el punto C. Estas rectas se dice también que son concurrentes o convergentes que significa que tienden a unirse o que la distancia entre ellas se va haciendo menor hasta cortarse en un punto.

LÍNEAS CONVERGENTES

Son las que saliendo de dos puntos del mismo plano, a medida que avanzan se juntan en un punto dado:

Como ves, las rectas han salido de los puntos A y B y si se prolongan, se juntarán en C.

LÍNEAS  DIVERGENTES

Son las que saliendo del mismo punto, a medida que avanzan se van separando una de otra:

Divergir o separarse es lo contrario de convergir.

Paralelas:  Las rectas paralelas no se cortan en ningún punto.

Coincidentes:  Dos rectas son coincidentes si todos sus puntos son comunes.

Perpendiculares: Dos rectas son perpendiculares cuando al cortarse forman cuatro ángulos iguales de 90º.

EJEMPLO 5:

 Hallar la recta del haz de centro ( 2 , 3/2) y que pasa por ( 0 , 3 ).

EJEMPLO 6:

Las rectas  r : x - 3y + 2 = 0  y  s : x + 2y - 1 = 0   forman parte de un haz. ¿ Cúal es la recta de ese haz que pasa por el punto ( 3 , -2 ) ?

7.3 ÁNGULOS

Ángulos

Se toma un punto del plano y partiendo de ese punto, se dibujan dos semirrectas. A la abertura formada por las dos semirrectas se le llama ángulo.

Definición de ángulo
Se llama ángulo a la parte del plano delimitada por dos semirrectas que parten de un mismo punto llamado vértice. A cada semirrecta se le llama lado del ángulo.

- Los lados del ángulo son las semirrectas que lo forman.
- El vértice del ángulo es el punto común que es origen de los lados.

Los tipos de ángulos son:
Agudo < 90°
Recto = 90°
Obtuso > 90°
Convexo < 180°
Llano = 180°
Cóncavo > 180°
Completo = 360°
Nulo = 0º
Hoy hablaremos de los ángulos agudo, recto y obtuso.

2- Tipos de ángulos según su medida
 

Agudo < 90°	Recto = 90°	Obtuso>90°

 

2.1- Ángulos rectos
Un ángulo recto es un ángulo que mide exactamente 90°. Si te das cuenta, en la esquina del ángulo hay un símbolo especial, una caja. Si ves ese símbolo, el ángulo es recto. No se suele escribir el 90°. Si ves la caja en la esquina ya te están diciendo que es un ángulo recto.

Un ángulo recto puede estar en cualquier orientación o giro, lo que importa es que el ángulo interior sea 90°

2.2- Ángulos agudos
Un ángulo agudo es un ángulo que mide menos de 90°. 

Acuérdate de fijarte en cuál de los dos ángulos es al que se refiere uno. Si el ángulo pequeño es menor que 90°, entonces ese es agudo.

2.3- Ángulos obtusos
Un ángulo obtuso es un ángulo que mide más de 90° pero menos de 180°. 

 

Acuérdate de fijarte en cuál de las dos partes es a la que se refiere uno. El ángulo más pequeño entre laslíneas es obtuso si mide entre 90° y 180°.
 

3. Algunas cosas importantes que hay que saber 
Los ángulos que miden 180° se denominan ángulos extendidos o llanos.

Los ángulos que miden más de 180° y menos de 360° se denominan ángulos cóncavos.

Los ángulos que miden 360° se denominan ángulos completos.

El ángulo nulo está formado por dos semirrectas coincidentes, por lo que su abertura es nula, es decir, 0°.
 

 

Los ángulos pueden nombrarse utilizando letras griegas. Por ejemplo:

 

 
EJEMPLO 7:



EJEMPLO 8:

7.4 POLIGONALES Y POLIGONOS

Un polígono es una figura plana y cerrada limitada por segmentos.

• Lados: son los segmentos que limitan la superficie.
• Vértices: son los puntos de unión de los segmentos.
• Ángulos:
  • Interiores: son las regiones, dentro de l a línea poligonal, creadas por dos lados consecutivos.
  • Exteriores: son las regiones, fuera de la línea poligonal, limitadas por dos lados consecutivos.
• Diagonales:Son los segmentos que unen dos vértices no consecutivos.

Clasificación de los polígonos según sus ángulos.

• Diermos que un polígono es convexo si todos sus ángulos interiores son menores de 180º.
• Diremos que un polígono es cóncavo si alguno de sus ángulos interiores es mayor de 180º.

Clasificación de polígonos según sus lados y ángulos.

• Diremos que un polígono es regular si tiene todos sus lados y sus ángulos iguales.
• Diremos que un polígono es irregular si tiene algún lado o ángulo distinto.

Clasificación de polígonos según su número de lados.

Nº de lados	Nombre	Regular
3	Triángulo
4	Cuadrilátero
5	Pentágono
6	Hexágono
7	Heptágono
8	Octógono
9	Eneágono
10	Decágono
11	Endecágono
12	Dodecágono

7.5 TRIÁNGULOS 

Clasificación de triángulos

Por sus lados.

• Triángulo equilátero : tiene los tres lados y los tres ángulos iguales.
• Triángulo isósceles: tiene dos lados y dos ángulos iguales.
• Triángulo escaleno: tiene los tres lados y los tres ángulos desiguales.

Por sus ángulos.

• Triángulo acutángulo: tiene los tres ángulos agudos.
• Triángulo rectángulo: tiene un ángulo recto.
• Triángulo obtusángulo: tiene un ángulo obtuso.

Triángulos rectángulos.

Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90º. Sus lados reciben nombres especiales:

• El lado opuesto al ángulo recto, se denomina hipotenusa.
• Los dos lados que forman el ángulo recto se denominan catetos.

Además, en todos los triángulos rectángulos se cumple que:

• La hipotenusa es mayor que cada uno de los catetos.
• Los ángulos agudos son complementarios ya que:

       

EJEMPLO 9:

7.6 CUADRILÁTEROS

Un cuadrilátero es un polígono de cuatro lados.

Paralelogramos.

Son cuadriláteros que tienen los lados paralelos dos a dos.

• Cuadrado: tiene los cuatro lados iguales y los cuatro ángulos rectos.
• Rectángulo: tiene los cuatro ángulos rectos.
• Rombo: tiene los cuatro lados iguales.
• Romboide: tiene los ángulos y los lados iguales, dos a dos, y no tiene ángulos rectos.

Trapecios.

Son cuadriláteros que tienen sólo dos lados paralelos.

• Rectángulo: tiene dos ángulos rectos.
• Isósceles: tiene dos lados iguales.
• Escaleno: no tiene lados iguales ni ángulos rectos.

Trapezoides.

Son cuadriláteros que no tienen ningún par de lados paralelos.

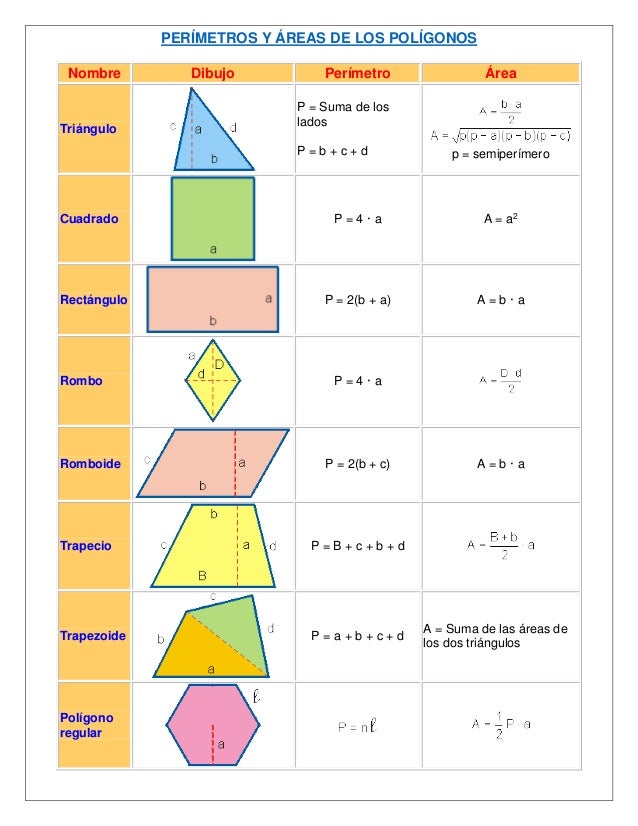
7.7 PERÍMETRO Y ÁREA DE UN POLÍGONO

EJERCICIO 10:

7.8 CIRCUNFERENCIA Y CIRCULO

En realidad la definición de circunferencia es "el conjunto de todos los puntos de un plano que están a una distancia fija de un centro".

Radio y diámetro El radio es la distancia del centro al borde. El diámetro empieza en un punto de la circunferencia, pasa por el centro y termina en el otro lado. Así que el diámetro es el doble del radio: Diámetro = 2 × Radio
Longitud de la circunferencia La circunferencia es la distancia alrededor del borde del círculo. Mide exactamente Pi (el símbolo es π) por el diámetro, o sea: Circunferencia = π × Diámetro Y estas fórmulas también: Circunferencia = 2 × π × Radio Circunferencia/Diámetro = π

Área del círculo El área del círculo es π por el cuadrado del radio, se escribe así: A = π × r2 O, en términos del diámetro: A = (π/4) × D2 Es fácil acordarse si piensas en el área del cuadrado en el que cabe el círculo.

Los círculos son objetos conocidos desde hace miles de años así que hay muchos nombres especiales.

Nadie quiere decir "la línea que empieza en un punto de la circunferencia, pasa por el centro y termina en el otro lado" cuando vale con decir "diámetro".

Aquí tienes los nombres especiales más comunes:

Líneas Una línea que va de un punto de la circunferencia a otro se llama cuerda. Si la línea pasa por el centro se llama diámetro. Si una línea "sólo toca" la circunferencia al pasar se llama tangente. Y una parte de una circunferencia se llama arco.

Trozos Hay dos tipos importantes de "trozos" de un círculo Un trozo "de pizza" se llama sector. Y un trozo marcado por una cuerda se llama segmento.

Sectores comunes

El cuadrante y el semicírculo son dos tipos especiales de sectores:

	Un cuarto de círculo se llama cuadrante. Medio círculo se llama semicírculo.

7.10 FIGURAS CIRCULARES

Hay diferentes formas de hacer partes de un círculo y algunas de ellas reciben nombres especiales.

Sector circular: Región del círculo limitada por dos radios y el arco que determinan.

Segmento circular: Región del círculo limitada por una cuerda y el arco correspondiente.

Zona circular: Región del círculo determinada por dos cuerdas paralelas.

Corona circular: Región del círculo limitada por dos circunferencias con céntricas.

Trapecio circular: Parte de una corona circular limitada por dos radios.

   

EJEMPLO 11:

EJEMPLO 12:

Calcular el perímetro y el área de las siguientes figuras coloreadas.