Decimos que un ángulo es la abertura que hay entre dos rectas (o segmentos) que se cortan en un punto llamado vértice.
En esta figura podemos observar la abertura creada por las dos rectas (simbolizada por los puntos discontinuos) y que representaría el ángulo formado.
TIPOS DE ÁNGULOS
Observaremos que hay diferentes tipos de ángulos. Los definimos a continuación:- Ángulo recto: es el ángulo formado por dos rectas dispuestas perpendicularmente.

- Ángulo agudo: es un ángulo menor que un ángulo recto.

- Ángulo llano: es el ángulo formado por dos rectas planas.

- Ángulo obtuso: es un ángulo menor que un ángulo llano pero mayor que un ángulo recto.

- Ángulo completo: es el ángulo formado por dos rectas superpuestas.

- Ángulo cóncavo: es un ángulo mayor que un ángulo obtuso pero menor que un ángulo completo.
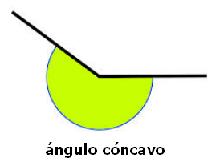
EJEMPLO 1
Un ángulo llano menos un ángulo recto resulta un ángulo recto:
Medida de ángulos
Los ángulos los medimos con grados y se simboliza con el signo (por ejemplo: 93 grados lo expresamos como 93º).
Para establecer esta medida dividimos lo que seria un ángulo completo en 360 grados, y a partir de esta definición podemos saber cuanto mide un grado.
Para entenderlo mejor recordemos que un ángulo completo es el ángulo formado por dos rectas que estén superpuestas:
Un ángulo completo es un ángulo de 360 grados.
Una vez establecida esta medida, podemos observar que:
- Un ángulo recto mide 90º.
- Un ángulo agudo mide entre0º y 90º.
- Un ángulo llano mide 180º .
- Un ángulo obtuso mide entre 90º y 180º.
- Un ángulo completo mide 360º.
- Un ángulo cóncavo mide entre 180ºy 360º .
EJERCICIO 2:
EJERCICIO 3:
EJERCICIO 4:
Bisectriz de un ángulo
Diremos que la bisectriz de un ángulo formado por dos rectas es el ángulo formado por una tercera recta que divide el ángulo original en dos ángulos idénticos:
En este dibujo podemos ver que la recta roja divide el ángulo formado por las otras dos rectas por la mitad.
Para calcular el ángulo formado por la recta bisectriz, simplemente se tendrá que dividir por dos el valor del ángulo inicial.
EJEMPLO 5:
Dividimos por dos 42 y encontramos que:
42º/2= 21º
Por consiguiente, la recta bisectriz tiene un ángulo de 21 grados
5.2 FUNCIONES TRIGONOMÉTRICAS ELEMENTALES
Las funciones trigonométricas básicas son el seno y el coseno. El resto de las funciones trigonométricas se obtiene a partir de ellas. Comenzamos con una definición informal. Un ángulo dirigido puede ser considerado como un par de semirrectas (l1,l2) con el mismo punto inicial.
EJEMPLO 6: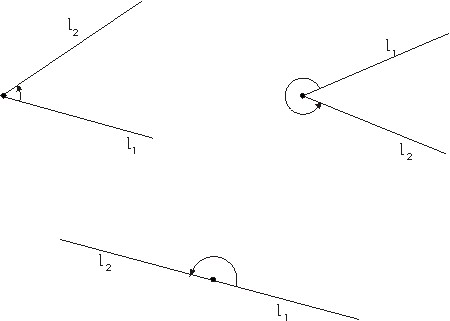 Si para l1 elegimos siempre la mitad positiva del eje horizontal, un ángulo dirigido vendrá descrito mediante la segunda semirrecta. Puesto que cada semirrecta corta al círculo unidad exactamente una vez, un ángulo dirigido queda descrito, aún más sencillamente, mediante un punto sobre el círculo unidad, es decir un punto (x,y) tal que x2+y2=1.
Si para l1 elegimos siempre la mitad positiva del eje horizontal, un ángulo dirigido vendrá descrito mediante la segunda semirrecta. Puesto que cada semirrecta corta al círculo unidad exactamente una vez, un ángulo dirigido queda descrito, aún más sencillamente, mediante un punto sobre el círculo unidad, es decir un punto (x,y) tal que x2+y2=1.
Entonces el seno del ángulo se define como la ordenada y del punto que lo representa y el coseno como la abcisa x, según se representa en la figura siguiente:
Sin embargo queremos definir el seno y el coseno de cualquier número real x .
El procedimiento usual es asociar un ángulo a cada número.
Esta asociación se lleva a cabo del modo siguiente: dado un número real cualquiera x, elíjase un punto P sobre el círculo unidad tal que x sea la longitud del arco de círculo que empieza en (1,0) y que se dirige hacia P en sentido contrario al de las agujas de un reloj.
El ángulo así construido determinado por P se denomina ángulo de x radianes. Al ser 2p la longitud total del círculo, el ángulo de x radianes y el ángulo de 2p +x radianes son idénticos.Se puede definir ahora el seno de x como el seno del ángulo de x radianes.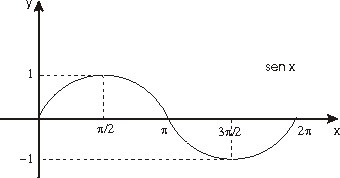
Esta definición se extiende primero al intervalo [-p , 0 ) de la forma siguiente:
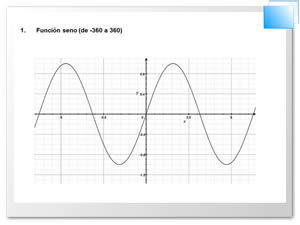
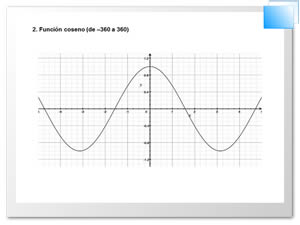
Por último, la definición de las funciones seno y coseno se extiende a toda la recta real de forma periódica.
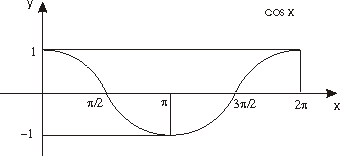
Las figuras siguientes muestran esta extensión.


Las funciones seno y coseno son continuas en IR y admiten derivada en todo punto verificándose que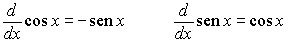 Además, son funciones acotadas puesto que verifican las siguientes igualdades:
Además, son funciones acotadas puesto que verifican las siguientes igualdades: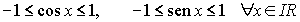 El resto de las funciones trigonométricas se definen como sigue:
El resto de las funciones trigonométricas se definen como sigue:
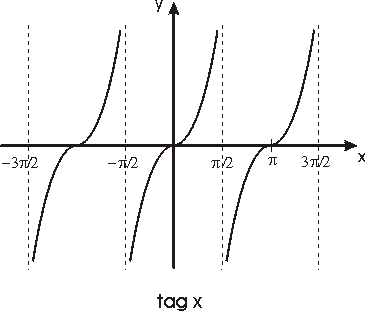
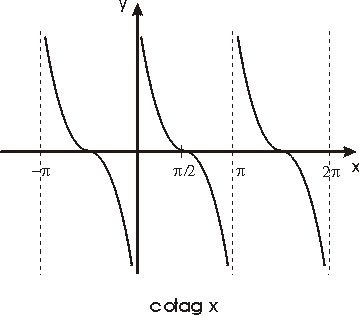
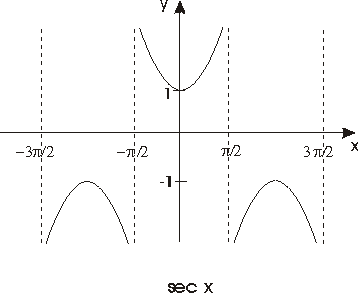
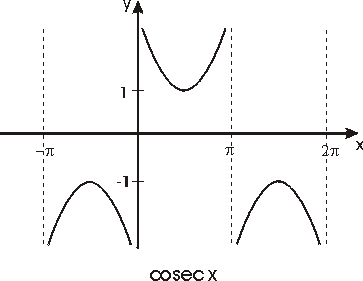
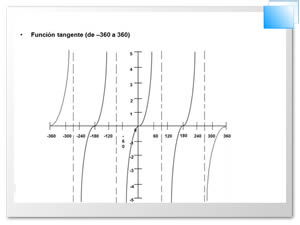
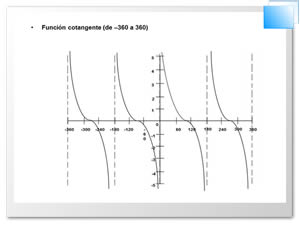
Véanse las gráficas de estas funciones en las figuras siguientes
Dado el siguiente Triángulo, encontrar todas las Funciones Trigonométricas en cada caso que se requiera, o las que hacen falta.
1. Primero encontraremos el valor de la ecuación que nos hace falta, en éste caso, ya que sabemos que la función de Coseno relaciona Lado Adyacente sobre Hipotenusa, ya conocemos dichos valores, nos faltaría encontrar Lado Opuesto:
2. Ahora conociendo el valor que nos hacía falta (b), empezaremos a encontrar cada una de las funciones que hacen falta:
3. Teniendo todas la Funciones procedemos a graficar:
EJEMPLO 7:
1. Resolvamos primero la Fracción Mixta 
Multiplicamos 2 x 3 y el resultado lo sumamos con el 1 dándonos como resultado 7/2.
2. Ahora encontramos el valor que hace falta:
Sustituimos valores:
3. Ahora conociendo b, encontramos las funciones correspondientes:
4. Seguidamente graficamos:
Tenemos un ángulo β equivalente a 25° 12 ' 42'', por lo que tenemos que pasarlo a Grados; Nos piden encontrar un ángulo y dos lados,
1. Comenzaremos a pasar los 25° 12 ' 42'' a Grados
2. Conociendo β, podemos conocer γ, ya que α = 90°, así:
3. Ahora, empezaremos a encontrar los lados que nos hacen falta, ya que conocemos γ, podemos encontrar el lado por medio de las funciones trigonométricas:
Despejemos la Variable: c Sen 64.79 ° =
Aplicamos por medio de la Calculadora La Función Seno de 64.79, que es : 0.9047527, luego dividimos 7 ÷ 0.9047527 = 7.73 = c.
4. Ahora conociendo el valor de c, podemos aplicar el Teorema de Pitágoras:
5. Quedando finalmente la gráfica así:
5.3 GRÁFICA DE FUNCIONES TRIGONOMÉTRICAS
Si queremos representar en forma gráfica una
función trigonométrica tomamos los valores de la variable independiente
como abscisas y los valores de la función como ordenadas, obteniendo
así una serie de puntos, los que al unirlos nos dará una línea que será
la representación gráfica de la función.
Uso de la función seno: ésta se usa cuando en un
triángulo rectángulo se conoce un ángulo agudo y el cateto opuesto, o un
ángulo agudo y la hipotenusa, o el cateto opuesto al ángulo dado.
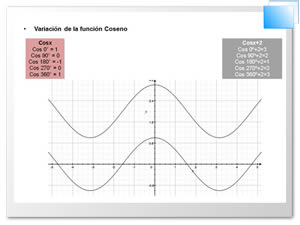
Uso de la función coseno: si en un triángulo rectángulo conocemos un ángulo agudo y el cateto adyacente, o un ángulo agudo y la hipotenusa.
Podemos calcular el cateto adyacente al ángulo dado y la hipotenusa usando esta función.
Uso de la función tangente: si en un triángulo rectángulo conocemos un cateto y el ángulo adyacente a él podemos calcular el otro cateto.
Uso de la función cotangente: por lo tanto en todo
triángulo rectángulo si conocemos un cateto y su ángulo opuesto podemos
calcular el valor del otro mediante ésta.
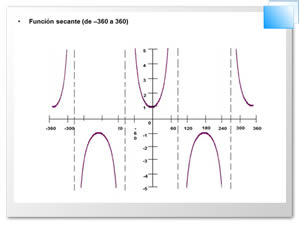
Uso de la función secante: ésta se usa cuando se tiene lo contrario que en la función coseno.
Uso de la función cosecante: ésta se usa cuando se tiene lo contrario a la función seno.
EJEMPLO 9:
EJEMPLO 9:
5.5 IDENTIDADES TRIGONOMETRICAS
Las identidades trigonométricas son igualdades que
involucran funciones trigonométricas. Estas identidades son siempre
útiles para cuando necesitamos simplificar expresiones que tienen
incluidas funciones trigonométricas, cualesquiera que sean los valores
que se asignen a los ángulos para los cuales están definidas estas
razones.Las identidades trigonométricas nos permiten plantear una misma
expresión de diferentes formas. Para simplificar expresiones
algebraicas, usamos la factorización, denominadores comunes, etc. Pero
para simplificar expresiones trigonométricas utilizaremos estas técnicas
en conjunto con las identidades trigonométricas.
Antes de comenzar a ver las diferentes identidades trigonométricas,
debemos conocer algunos términos que usaremos bastante en trigonometría,
que son las tres funciones más importantes dentro de esta. El coseno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto adyacente y la hipotenusa:
Otra función que utilizaremos en trigonometría es “seno”. Definiremos seno como la razón entre el cateto opuesto y la hipotenusa en un triángulo rectángulo:
Mientras tanto la palabra tangente en matemática puede
que tenga dos significados distintos. En geometría se utiliza el término
de recta tangente, pero a nosotros en trigonometría nos interesa otro
término que es el de tangente de un ángulo, el cual es la relación entre
los catetos de un triángulo rectángulo , lo mimo que decir que es el
valor numérico que resulta de dividir la longitud del cateto opuesto
entre la del cateto adyacente al ángulo.
Las siguientes identidades se cumplen para cualquier ángulo en el cual el denominador no sea cero. Estas son identidades recíprocas:
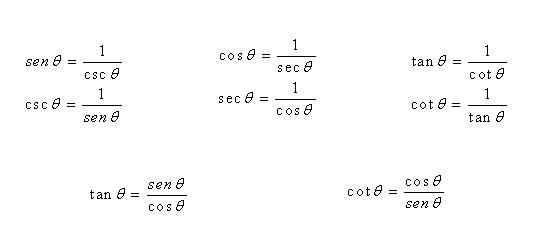
A partir de las relaciones pitagóricas es posible
encontrar otras identidades y demostrar algunas identidades
trigonométricas. Mediante estas relaciones si conocemos las medidas de
los catetos de un triángulo rectángulo podemos calcular la medida de la
hipotenusa (lado opuesto al ángulo recto) y si conocemos la medida de la
hipotenusa y la de un cateto podemos calcular la medida del otro
cateto. Entonces diremos que el teorema de Pitágoras es un teorema que
se aplica únicamente a triángulos rectángulos, y nos sirve para obtener
un lado o la hipotenusa de un triángulo, si es que se conocen los otros
dos. Las identidades de relaciones pitagóricas son las siguientes:

De acuerdo al teorema de pitágoras :
Ahora veremos algunos ejemplos.
EJEMPLO:
Como primer ejemplo verificaremos la siguiente identidad:
EJEMPLO:
Como primer ejemplo verificaremos la siguiente identidad:
Obtendremos la solución utilizando las identidades recíprocas:
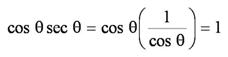
Observemos también el siguiente ejemplo, en el cual verificaremos otra identidad:
Su solución :
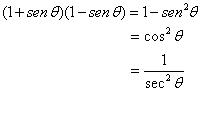
Otra de las identidades trigonométricas sería la de división:
Las siguientes identidades serían las de suma y diferencia de dos ángulos:
Tenemos también las identidades de suma y diferencia del seno y coseno de dos ángulos, aquí las tenemos:
Identidad trigonométrica de producto del seno y el coseno de dos ángulos:
Identidades trigonométricas de ángulo doble:
Identidades trigonométricas de mitad de ángulo:
Por último observaremos algunas otras identidades trigonométricas :
- 1Relación seno coseno
cos² α + sen² α = 1
- 2Relación secante tangente
sec² α = 1 + tg² α
- 3Relación cosecante cotangente
cosec² α = 1 + cotg² α
EJEMPLO 10:
Comprobar las identidades trigonométricas:
1


EJEMPLO 11:
2


EJEMPLO 12:
3

EJEMPLO 10:
Comprobar las identidades trigonométricas:
1
EJEMPLO 11:
2
EJEMPLO 12:
3



No hay comentarios.:
Publicar un comentario